Need a formula for composing two feasibility relations in series.
Suppose \(P,Q,R\) are cities (preorders) and there are bridges (hence, feasibility matrices).
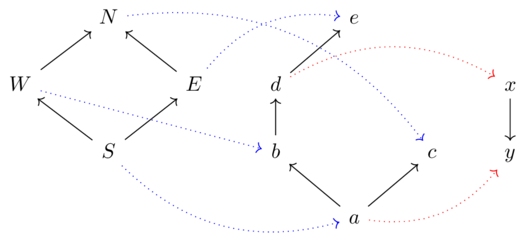
The feasibility matrices are:
| \(\textcolor{blue}{\phi}\) | a | b | c | d | e |
|---|---|---|---|---|---|
| N | T | F | T | F | F |
| E | T | F | T | F | T |
| W | T | T | T | T | F |
| S | T | T | T | T | T |
| \(\textcolor{red}{\psi}\) | x | y |
|---|---|---|
| a | F | T |
| b | T | T |
| c | F | T |
| d | T | T |
| e | F | F |
Feasibility from \(P\) to \(R\) means there is a way-point in Q which is both reachable from \(p \in P\) and can reach \(r \in R\).
Composition is a union \((\phi;\psi)(p,r):= \bigvee_Q \phi(p,q)\land \psi(q,r)\).
But this is tantamount to matrix multiplication which gives us the result matrix:
| \(\phi;\psi\) | x | y |
|---|---|---|
| N | F | T |
| E | F | T |
| W | T | T |
| S | T | T |